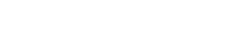Τουλάχιστον 5 δισεκατομμύρια πίτσες πωλούνται σε όλο τον κόσμο κάθε χρόνο και 350 κομμάτια καταναλώνονται κάθε δευτερόλεπτο, αλλά πόσα από αυτά είναι ίσα;
Δύο μαθηματικοί αποκάλυψαν ότι το να κόψεις μια πίτσα σωστά δεν είναι απλά μια μορφή τέχνης, αλλά βασίζεται στη γεωμετρία.
Προηγούμενη έρευνα έδειξε ότι είναι δυνατό να κόψεις σε 12 ίσα κομμάτια μια πίτα, αλλά αυτή η δυάδα το πήγε ένα βήμα παρακάτω και απέδειξε ότι δεν υπάρχει όριο στο πόσα ίδια κομμάτια μπορούν να κοπούν σε μια πίτσα.
Ο Joel Haddley και ο Stephen Worsley, από το Πανεπιστήμιο του Liverpool εφηύραν την προηγούμενη μέθοδο για το κόψιμο του τέλειου κομματιού, γνωστού και ως πλακίδια μονοεδρικού δίσκου, το οποίο έχει ως αποτέλεσμα 12 ίδια κομμάτια.
Η διαδικασία ξεκινά κόβοντας ένα κομμάτι σε έξι κομμάτια με 3 καμπύλες πλευρές σε όλη την πίτσα.
Αν γίνει σωστά, θα μοιάζει σαν αστέρι που βγαίνει από το κέντρο.
Μετά, μοιράζεις τα σχήματα στα δύο, καταλήγοντας σε δύο ομάδες κομματιών: μία μέσα χωρίς κόρα, και μία έξω με κόρα.
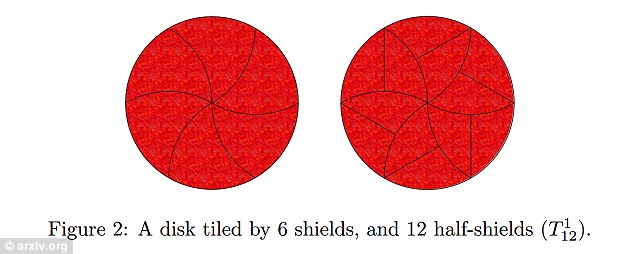
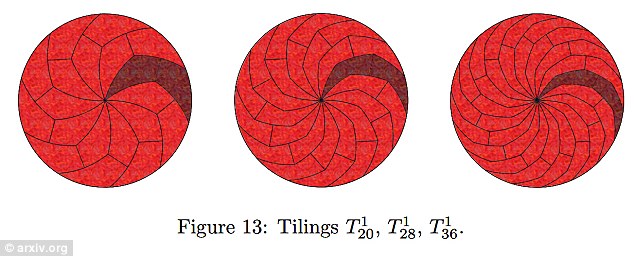
Η ομάδα πήγε την έρευνα ένα βήμα παρακάτω και έκοψε ακόμα περισσότερα κομμάτια δημιουργώντας παρόμοια πλακίδια με περιττό αριθμό πλευρών – γνωστά ως πεντάγωνα, εφτάγωνα, κλπ – και μετά τα μοίρασε στα δύο σύμφωνα με την προηγούμενη μέθοδο, όπως αναφέρει το New Scientist.
«Μαθηματικά δεν υπάρχει κανένα όριο», είπε ο Haddley στο New Scientist, «αν και μπορεί να μην είναι πρακτικό να συνεχιστούν τα κομμάτια να κόβονται σε παραπάνω από 9γωνα.»
Στη συνέχεια έγιναν εγκοπές στις γωνίες των σχημάτων για να σχηματιστούν αγκαθωτά κομμάτια στην κυκλική πίτα.
«Δεν έχω ιδέα αν υπάρχουν άλλες εφαρμογές της δουλειάς μας πέρα από το κόψιμο της πίτσας», είπε ο Haddley, ο οποίος έχει προσπαθήσει να κόψει μια πίτσα με αυτό τον τρόπο.
Αλλά είπε, «Τα αποτελέσματα έχουν μαθηματικό ενδιαφέρον και μπορούν να δημιουργήσουν κάποιες ωραίες εικόνες.»
Σύμφωνα με τους ερευνητές, μπορείς να συνεχίσεις να κόβεις την πίτσα αόριστα και αν έχεις όρεξη για πειραματισμούς μπορείς να προσθέσεις περισσότερες εγκοπές και πιο παράξενα κομμάτια.
Μία άλλος μαθηματικός αντιμετώπισε έναν ακόμα γρίφο το 2013 και δημοσίευσε μια έρευνα η οποία ισχυρίζεται ότι έχει εφεύρει την πρώτη φόρμουλα για την «τέλεια μοιρασμένη» πίτσα, λαμβάνοντας υπόψη παράγοντες όπως η αναλογία υλικών στην βάση.
Η Dr Eugenia Cheng είπε ότι οι λάτρεις της πίτσας θέλουν περισσότερα υλικά σε κάθε μπουκιά, σε μικρότερη πίτσα, αλλά πιο μοιρασμένες μπουκιές σε μεγαλύτερη πίτσα.
Η μαθηματικός από το πανεπιστήμιο του Sheffield υπολόγισε την αναλογία για να εξασφαλίσει την μέγιστη γεύση από τα υλικά στη βάση.
Φαίνεται ότι ακόμα και αν ένα άτομο κρατάει την ίδια ποσότητα ζύμης και υλικών, η αναλογία υλικών στη βάση σε μια μέση μπουκιά αλλάζει με το μέγεθος της πίτσας και οι μικρότερες έχουν περισσότερα υλικά ανά μπουκιά παρά οι μεγαλύτερες.
Η Dr Cheng είπε ότι δεν έχει να κάνει μόνο με το πόσο χοντρή είναι η βάση, αλλά και με την ισορροπία των γεύσεων ανάμεσα στα υλικά και τη ζύμη, η οποία καθορίζει πόσα υλικά μπορεί να απολαύσει ένα άτομο ανά μπουκιά.
Χρησιμοποίησε το d σαν σταθερό όγκο της ζύμης και το t σαν σταθερό όγκο των υλικών για να εφεύρει μια μαθηματική φόρμουλα για την αναλογία υλικών στη βάση σε μια μέση μπουκιά.
Η Dr Cheng υπολόγισε ότι με σχετικούς όρους, η μέση μπουκιά από μια πίτσα 28 εκατοστών έχει 10% περισσότερα υλικά από τη μέση μπουκιά μιας πίτσας 36 εκατοστών.
Η φόρμουλα επίσης αποκαλύπτει ότι αν και οι μικρότερες πίτσες έχουν περισσότερα υλικά ανά μπουκιά, για αυτούς που μαγειρεύουν στο σπίτι και αναζητούν πολλά παραπάνω στις δημιουργίες τους, υπάρχει μεγαλύτερος κίνδυνος η πίτσα τους να έχει μουλιασμένη βάση.
Δημιούργησε μια άλλη φόρμουλα, alpha, διαιρεμένη από την ακτίνα της πίτσας, τετραγωνισμένη για να υπολογίσει το μέγεθος της κόρας για πίτσες διαφορετικών μεγεθών.
Εξηγεί ότι το μέγεθος της κόρας είναι ανάλογο με το πάχος της πίτσας – όσο πιο μεγάλη είναι η πίτσα, τόσο πιο λεπτή ή βάση, άρα πιο μικρή η κόρα.
Υπολόγισε την αξία του alpha σε 15 πειράματα, κάνοντας μερικές πίτσες διαφόρων μεγεθών.
Η μαθηματικός εφηύρε αυτές τις φόρμουλες επειδή της ζήτησε η αλυσίδα εστιατορίων PizzaExpress να βρει γιατί η πίτσα Romana 36 εκατοστών, η οποία έχει πιο λεπτή και τραγανή βάση από την κλασική πίτσα 28 εκατοστών, είναι τόσο δημοφιλής.
Η Dr. Cheng βρήκε ότι το μυστικό βρίσκεται στις αναλογίες της πίτσας των 36 εκατοστών, αφού μαγειρεύεται το ίδιο ομοιόμορφα με την μικρότερη έκδοση, αλά τα υλικά μοιράζονται σε μεγαλύτερη επιφάνεια πιο κοντά στην άκρη της πίτσας.
Ωστόσο, τεχνικά, οι λάτρεις της πίτσας που αναζητούν περισσότερα υλικά ανά μπουκιά θα έπρεπε να διαλέγουν την κλασική πίτσα 28 εκατοστών, με βάση την έρευνα.

Είπε: «Πάντα αναζητώ τρόπους για να φέρω το φαγητό και τα μαθηματικά κοντά, αφού είναι δύο από τα αγαπημένα μου πράγματα, αλλά οι περισσότεροι προτιμούν το φαγητό.»
«Μου αρέσει να δείχνω ότι τα μαθηματικά είναι παντού στον κόσμο γύρω μας, και ότι μπορούμε να χρησιμοποιήσουμε τα μαθηματικά για να δώσουμε λογική εξήγηση για κάτι που ανακαλύψαμε με το ένστικτο μας, όπως ότι οι μικρότερες πίτσες διατρέχουν περισσότερο κίνδυνο να έχουν μουλιασμένη βάση!»
Η Rebecca Farrer, διευθύντρια του εμπορικού σήματος του PizzaExpress, είπε ότι τα εστιατόρια της αλυσίδας μπορεί να μην ξέρουν ότι «είναι το ζυμάρι μας, το πώς οι μάγειρες μας το τεντώνουν και το πώς μοιράζουν τα υλικά που κάνει τη διαφορά, βεβαιώνοντας ότι η αγαπημένη τους πίτσα ψήνεται τέλεια κάθε φορά».
Το PizzaExpress κάνει για πρώτη φορά από το 1965 μικροαλλαγές στη ζύμη, προσθέτοντας 15 γραμμάρια στις συνταγές του για πίτσα.
«Μπορεί να μη φαίνεται πολύ, αλλά σημαίνει ότι το πάχος της Romana, η οποία στρώνεται με πλάστη για να υπάρχει ίση ποσότητα ζύμης σε όλη τη βάση και καθόλου αέρας, είναι πιο σταθερό από πριν», λέει η κυρία Farrer.
«Για αυτούς που αγαπούν την πίτσα όπως εμείς, 15 γραμμάρια κάνουν όλη τη διαφορά», προσθέτει.
Credit: dailymail.co.uk